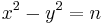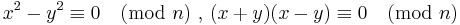Congruence of squares

In number theory, a congruence of squares is a congruence commonly used in integer factorization algorithms.

Derivation

Given a positive integer n, Fermat's factorization method relies on finding numbers x, y satisfying the equality

$x^2 - y^2 = n\,\!$

We can then factor n = x² − y² = (x + y) (x − y). However, this algorithm is slow in practice because we need to search many such numbers, and only a few satisfy this strict equation. However, n can also be factored if we satisfy the weaker congruence of squares

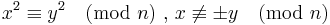$x^2 \equiv y^2 \pmod{n} \hbox{ , } x \not\equiv \pm y \pmod{n}$ .

From here we easily deduce

$x^2 - y^2 \equiv 0 \pmod{n} \hbox{ , } (x %2B y)(x - y) \equiv 0 \pmod{n}$

This means that n divides (x + y) (x − y). However we have required that x ≠ ±y (mod n), so n divides neither (x+y) nor (x−y) alone. Thus (x+y) and (x−y) each contain proper factors of n. Computing the greatest common divisors of (x + y, n) and of (x − y, n) will give us these factors; this can be done quickly using the Euclidean algorithm.

Congruences of squares are extremely useful in integer factorization algorithms. This congruence is extensively used in, for example, the quadratic sieve, general number field sieve, continued fraction factorization, Dixon's factorization, and so on. Conversely, because finding square roots modulo a composite number is probabilistic polynomial-time equivalent to factoring that number, any integer factorization algorithm can be used to efficiently identify a congruence of squares.

Example

We take n = 35. We find that

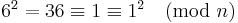$\textstyle 6^2 = 36 \equiv 1 \equiv 1^2 \pmod{n}$ .

We can thus factor 35 as gcd(6 − 1, 35) = 5 and gcd(6 + 1, 35) = 7.

Further generalizations

We can also use factor bases to help us find congruences of squares more quickly. Instead of looking for 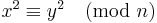$\textstyle x^2 \equiv y^2 \pmod{n}$ from the outset, we find many 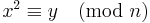$\textstyle x^2 \equiv y \pmod{n}$ where the y have small prime factors, and try to multiply a few of these together to get a square on the right-hand side.